Hinweis
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, sich anzumelden oder das Verzeichnis zu wechseln.
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, das Verzeichnis zu wechseln.
Alle Miningmodelle verwenden dieselbe Struktur, um ihre Inhalte zu speichern. Diese Struktur wird gemäß dem Data Mining-Inhaltsschema-Rowset definiert. Innerhalb dieser Standardstruktur werden die Knoten, die Informationen enthalten, jedoch auf unterschiedliche Weise angeordnet, um verschiedene Arten von Bäumen darzustellen. In diesem Thema wird beschrieben, wie die Knoten organisiert sind und was jeder Knoten bedeutet, für Miningmodelle, die auf dem Microsoft Time Series-Algorithmus basieren.
Eine Erläuterung allgemeiner Miningmodellinhalte, die für alle Modelltypen gelten, finden Sie unter Mining Model Content (Analysis Services - Data Mining).
Wenn Sie dieses Thema überprüfen, könnte es hilfreich sein, parallel den Inhalt eines Zeitreihenmodells zu durchstöbern. Sie können ein Zeitreihenmodell erstellen, indem Sie das Lernprogramm "Grundlegendes Data Mining" abschließen. Das Modell, das Sie im Lernprogramm erstellen, ist ein gemischtes Modell, das Daten mithilfe der Algorithmen ARIMA und ARTXP trainiert. Weitere Informationen finden Sie unter Erstellen einer Vorhersagestruktur und eines Modells (Fortgeschrittenes Data-Mining-Tutorial). Informationen zum Anzeigen des Inhalts eines Miningmodells finden Sie unter Data Mining Model Viewers.
Grundlegendes zur Struktur eines Zeitreihenmodells
Ein Zeitreihenmodell verfügt über einen einzelnen übergeordneten Knoten, der das Modell und seine Metadaten darstellt. Unterhalb dieses übergeordneten Knotens gibt es je nach dem Algorithmus, den Sie zum Erstellen des Modells verwendet haben, ein oder zwei Zeitreihenbäume.
Wenn Sie ein gemischtes Modell erstellen, werden dem Modell zwei separate Bäume hinzugefügt, ein Baum für ARIMA und ein Baum für ARTXP. Wenn Sie nur den ARTXP-Algorithmus oder nur den ARIMA-Algorithmus verwenden, verfügen Sie über eine einzelne Struktur, die diesem Algorithmus entspricht. Sie geben an, welcher Algorithmus verwendet werden soll, indem Sie den FORECAST_METHOD-Parameter festlegen. Weitere Informationen dazu, ob ARTXP, ARIMA oder ein gemischtes Modell verwendet werden soll, finden Sie unter Microsoft Time Series Algorithm.
Das folgende Diagramm zeigt ein Beispiel für ein Data Mining-Modell für Zeitreihen, das mit den Standardeinstellungen erstellt wurde, um ein gemischtes Modell zu erstellen. Damit Sie die Unterschiede zwischen den beiden Modellen einfacher vergleichen können, wird hier das ARTXP-Modell auf der linken Seite des Diagramms angezeigt, und das ARIMA-Modell wird auf der rechten Seite des Diagramms angezeigt. Während ARTXP eine strukturähnliche Struktur ist, die sich in kleinere und kleinere Verzweigungen aufteilt, ist die vom ARIMA-Algorithmus erstellte Struktur eher wie eine Pyramide, die von kleineren Komponenten nach oben aufgebaut ist.
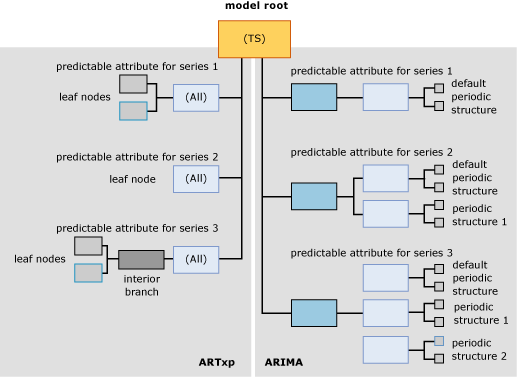
Wichtig ist, dass Informationen in den ARIMA- und ARTXP-Strukturen auf völlig unterschiedliche Weise angeordnet werden, und Sie sollten die beiden Strukturen nur im Stammknoten als verknüpft betrachten. Obwohl die beiden Darstellungen in einem Modell zur Bequemlichkeit präsentiert werden, sollten sie als zwei unabhängige Modelle behandelt werden. ARTXP stellt eine tatsächliche Baumstruktur dar, aber ARIMA tut dies nicht.
Wenn Sie den Microsoft Generic Model Content Tree Viewer verwenden, um ein Modell anzuzeigen, das ARIMA und ARTXP verwendet, werden die Knoten für die ARTXP- und ARIMA-Modelle als untergeordnete Knoten des übergeordneten Zeitreihenmodells dargestellt. Sie können sie jedoch ganz einfach durch die Bezeichnungen unterscheiden, die auf die Knoten angewendet werden.
Der erste Satz von Knoten wird mit der Bezeichnung "Alle" bezeichnet und stellt die Ergebnisse der Analyse durch den ARTXP-Algorithmus dar.
Der zweite Satz von Knoten ist ARIMA bezeichnet und stellt die Ergebnisse der Analyse durch den ARIMA-Algorithmus dar.
Warnung
Der Name (Alle) wird in der ARTXP-Baumstruktur nur aus Gründen der Abwärtskompatibilität beibehalten. Vor SQL Server 2008 verwendete der Zeitreihenalgorithmus einen einzelnen Algorithmus für die Analyse, den ARTXP-Algorithmus.
In den folgenden Abschnitten wird erläutert, wie die Knoten innerhalb der einzelnen Modelltypen angeordnet werden.
Struktur eines ARTXP-Modells
Der ARTXP-Algorithmus erstellt ein Modell, das einem Entscheidungsstrukturenmodell ähnelt. Es gruppiert vorhersagbare Attribute und teilt sie, wenn erhebliche Unterschiede gefunden werden. Daher enthält jedes ARTXP-Modell für jedes vorhersagbare Attribut eine separate Verzweigung. Beispielsweise erstellt das Lernprogramm "Data Mining basic" ein Modell, das den Umsatz für mehrere Regionen vorhersagt. In diesem Fall ist [Amount] das vorhersagbare Attribut und für jede Region wird eine separate Verzweigung erstellt. Wenn Sie zwei vorhersagbare Attribute haben: [Amount] und [Menge], wird für jede Kombination eines Attributs und einer Region eine separate Verzweigung erstellt.
Der obere Knoten für den ARTXP-Zweig enthält dieselben Informationen, die sich in einem Entscheidungsstrukturstammknoten befinden. Dies umfasst die Anzahl der untergeordneten Elemente für diesen Knoten (CHILDREN_CARDINALITY), die Anzahl der Fälle, die den Bedingungen dieses Knotens (NODE_SUPPORT) entsprechen, und eine Vielzahl beschreibender Statistiken (NODE_DISTRIBUTION).
Wenn der Knoten keine Kindknoten aufweist, bedeutet dies, dass keine signifikanten Bedingungen gefunden wurden, die eine Einteilung der Fälle in weitere Untergruppen rechtfertigen würden. Der Zweig endet an diesem Punkt und der Knoten wird als Blattknoten bezeichnet. Der Blattknoten enthält die Attribute, Koeffizienten und Werte, die die Bausteine der ARTXP-Formel sind.
Einige Zweige können zusätzliche Teilungen aufweisen, ähnlich wie ein Entscheidungsbaummodell. So teilt sich beispielsweise der Zweig des Baumes, der den Umsatz für die Region Europa darstellt, in zwei Zweige auf. Eine Spaltung tritt auf, wenn eine Bedingung gefunden wird, die einen erheblichen Unterschied zwischen den beiden Gruppen verursacht. Der übergeordnete Knoten teilt Ihnen den Namen des Attributs mit, das die Aufteilung verursacht hat, z. B. [Amount], und wie viele Fälle im übergeordneten Knoten vorhanden sind. Die Blattknoten enthalten weitere Details: den Wert des Attributs, z. B. [Sales] >10.000 vs. [Sales] < 10.000), die Anzahl der Fälle, die jede Bedingung unterstützen, und die ARTXP-Formel.
Hinweis
Wenn Sie die Formeln anzeigen möchten, finden Sie die vollständige Regressionsformel auf der Ebene des Blattknotens, aber nicht in einem Zwischen- oder Stammknoten.
Struktur eines ARIMA-Modells
Der ARIMA-Algorithmus erstellt für jede Kombination einer Datenreihe (z. B. [Region]) und eines vorhersagbaren Attributs (z. B. [Sales Amount]) einen einzelnen Informationsabschnitt, der die Änderung des vorhersagbaren Attributs im Laufe der Zeit beschreibt.
Die Formel für jede Datenreihe wird von mehreren Komponenten abgeleitet, eine für jede periodische Struktur, die in den Daten gefunden wurde. Wenn Sie beispielsweise Umsatzdaten haben, die monatlich gesammelt werden, kann der Algorithmus monatliche, vierteljährliche oder jährliche periodische Strukturen erkennen.
Der Algorithmus gibt für jede gefundene Periodizität einen separaten Satz von übergeordneten und untergeordneten Knoten aus. Die Standard-Periodizität ist 1, für ein einzelnes Zeitsegment und wird automatisch zu allen Modellen hinzugefügt. Sie können mögliche periodische Strukturen angeben, indem Sie mehrere Werte in den parameter PERIODICITY_HINT eingeben. Wenn der Algorithmus jedoch keine regelmäßige Struktur erkennt, gibt er keine Ergebnisse für diesen Hinweis aus.
Jede periodische Struktur, die im Modellinhalt ausgegeben wird, enthält die folgenden Komponentenknoten:
Ein Knoten für die autoregressive Reihenfolge (AR)
Ein Knoten für den gleitenden Durchschnitt (MA)
Informationen zur Bedeutung dieser Begriffe finden Sie im Microsoft-Zeitreihenalgorithmus.
Die Differenzreihenfolge ist ein wichtiger Bestandteil der Formel und wird in der Formel dargestellt. Weitere Informationen zur Verwendung der Differenzreihenreihenfolge finden Sie in der technischen Referenz zu Microsoft Time Series Algorithm.
Modellinhalt für Zeitreihen
Dieser Abschnitt enthält Details und Beispiele nur für die Spalten im Miningmodellinhalt, die für Zeitreihenmodelle eine besondere Relevanz haben.
Informationen zu allgemeinen Spalten im Schema-Rowset, z. B. MODEL_CATALOG und MODEL_NAME, oder erläuterungen der Miningmodellterminologie finden Sie unter Mining Model Content (Analysis Services - Data Mining).
MODELL_KATALOG
Name der Datenbank, in der das Modell gespeichert ist.
MODEL_NAME
Name des Modells.
ATTRIBUTE_NAME
Das vorhersagbare Attribut für die im Knoten dargestellte Datenreihe. (Derselbe Wert wie für MSOLAP_MODEL_COLUMN.)
NODE_NAME
Der Name des Knotens.
Derzeit enthält diese Spalte denselben Wert wie NODE_UNIQUE_NAME, obwohl sich dies in zukünftigen Versionen ändern kann.
NODE_UNIQUE_NAME
Der eindeutige Name des Knotens. Der übergeordnete Modellknoten hat immer den Namen TS.
ARTXP: Jeder Knoten wird durch TS gefolgt von einem hexadezimalen numerischen Wert dargestellt. Die Reihenfolge der Knoten ist unwichtig.
Beispielsweise können die ARTXP-Knoten direkt unter dem TS-Baum TS00000001-TS0000000b nummeriert sein.
ARIMA: Jeder Knoten in einer ARIMA-Struktur wird durch TA gefolgt von einem hexadezimalen numerischen Wert dargestellt. Die untergeordneten Knoten enthalten den eindeutigen Namen des übergeordneten Knotens gefolgt von einer weiteren hexadezimalen Zahl, die die Sequenz innerhalb des Knotens angibt.
Alle ARIMA-Bäume sind genau gleich strukturiert. Jeder Stamm enthält die Knoten und Benennungskonventionen, die in der folgenden Tabelle veranschaulicht werden:
| ARIMA Node ID und Typ | Beispiel für Knotenname |
|---|---|
| ARIMA-Wurzel (27) | TA00000000b |
| ARIMA Periodische Struktur (28) | TA00000000b0000000000 |
| ARIMA Auto Regressiv (29) | TA0000000b000000000 |
| ARIMA Gleitender Durchschnitt (30) | TA0000000b000000001 |
NODE_TYPE
Ein Zeitreihenmodell gibt je nach Algorithmus die folgenden Knotentypen aus.
ARTXP:
| Knotentyp-ID | BESCHREIBUNG |
|---|---|
| 1 (Modell) | Zeitreihe |
| 3 (Innenbereich) | Stellt einen Innenzweig innerhalb einer ARTXP-Zeitreihenstruktur dar. |
| 16 (Zeitreihenbaum) | Stamm des ARTXP-Baums, der einem vorhersagbaren Attribut und einer vorhersagbaren Datenreihe entspricht. |
| 15 (Zeitreihe) | Blattknoten im ARTXP-Baum. |
ARIMA:
| Knotentyp-ID | BESCHREIBUNG |
|---|---|
| 27 (ARIMA-Stamm) | Der oberste Knoten einer ARIMA-Baumstruktur. |
| 28 (ARIMA Periodische Struktur) | Komponente eines ARIMA-Baums, die eine einzelne periodische Struktur beschreibt. |
| 29 (ARIMA Autoregressive) | Enthält einen Koeffizienten für eine einzelne periodische Struktur. |
| 30 (ARIMA Gleitender Durchschnitt) | Enthält einen Koeffizienten für eine einzelne periodische Struktur. |
NODE_BESCHRIFTUNG
Eine Beschriftung oder ein Untertitel, die dem Knoten zugeordnet ist.
Diese Eigenschaft dient vor allem zu Darstellungszwecken.
ARTXP: Enthält die geteilte Bedingung für den Knoten, die als Kombination aus Attribut und Wertbereich angezeigt wird.
ARIMA: Enthält die kurze Form der ARIMA-Formel.
Informationen zum Format der ARIMA-Gleichung finden Sie unter Mining Legend for ARIMA.
Kinderanzahl
Die Anzahl der direkten Kinder, die der Knoten hat.
PARENT_UNIQUE_NAME
Der eindeutige Name des übergeordneten Knotens. NULL wird für alle Knoten auf der Stammebene zurückgegeben.
Knotenbeschreibung
Eine textliche Beschreibung der Regeln, Teilungen oder Formeln im aktuellen Knoten.
ARTXP: Weitere Informationen finden Sie unter Grundlegendes zur ARTXP-Struktur.
ARIMA: Weitere Informationen finden Sie unter Grundlegendes zur ARIMA-Struktur.
NODE_RULE
Eine XML-Beschreibung der Regeln, Aufteilungen oder Formeln im aktuellen Knoten.
ARTXP: Die NODE_RULE entspricht im Allgemeinen dem NODE_CAPTION.
ARIMA: Weitere Informationen finden Sie unter Grundlegendes zur ARIMA-Struktur.
MARGINAL_REGEL
Eine XML-Beschreibung der Teilung oder des Inhalts, die für diesen Knoten spezifisch ist.
ARTXP: Die MARGINAL_RULE entspricht im Allgemeinen dem NODE_DESCRIPTION.
ARIMA: Immer leer; verwenden Sie stattdessen NODE_RULE.
KNOTENWAHRSCHEINLICHKEIT
ARTXP: Bei Baumknoten immer 1. Für Blattknoten wird die Wahrscheinlichkeit beschrieben, dass der Knoten vom Modellstammknoten aus erreicht wird.
ARIMA: Immer 0.
Marginalwahrscheinlichkeit
ARTXP: Bei Baumknoten immer 1. Die Wahrscheinlichkeit, einen Blattknoten vom unmittelbar übergeordneten Knoten aus zu erreichen.
ARIMA: Immer 0.
KNOTENVERTEILUNG
Eine Tabelle, die das Wahrscheinlichkeits histogramm des Knotens enthält. In einem Zeitreihenmodell enthält diese geschachtelte Tabelle alle Komponenten, die zum Zusammenstellen der tatsächlichen Regressionsformel erforderlich sind.
Weitere Informationen zur Knotenverteilungstabelle in einer ARTXP-Struktur finden Sie unter Grundlegendes zur ARTXP-Struktur.
Weitere Informationen zur Knotenverteilungstabelle in einer ARIMA-Struktur finden Sie unter Grundlegendes zur ARIMA-Struktur.
Wenn Sie alle Konstanten und anderen Komponenten anzeigen möchten, die in einem lesbaren Format zusammengesetzt sind, verwenden Sie den Zeitreihen-Viewer, klicken Sie auf den Knoten, und öffnen Sie die Mininglegende.
Node-Unterstützung
Die Anzahl der Fälle, die diesen Knoten unterstützen.
ARTXP: Gibt für den Knoten (Alle) die Gesamtanzahl der Zeitsegmente an, die in der Verzweigung enthalten sind.
Gibt für Terminalknoten die Anzahl der Zeitsegmente an, die im Bereich enthalten sind, der durch NODE_CAPTION beschrieben wird. Die Anzahl der Zeitsegmente in den Terminalknoten summiert sich immer auf den NODE_SUPPORT Wert des Verzweigungsknotens (Alle).
ARIMA: Anzahl der Fälle, die die aktuelle periodische Struktur unterstützen. Der Wert für die Stütze wird in allen Knoten der gegenwärtigen periodischen Struktur wiederholt.
MSOLAP_MODEL_COLUMN
Das vorhersagbare Attribut für die im Knoten dargestellte Datenreihe. (Derselbe Wert wie für ATTRIBUTE_NAME.)
MSOLAP_NODE_SCORE
Ein numerischer Wert, der den Informationswert des Baums oder der Teilung kennzeichnet.
ARTXP: Der Wert ist immer 0,0 für Knoten ohne Unterbrechung. Bei Knoten mit einer Teilung stellt der Wert die Interessantesbewertung der Teilung dar.
Weitere Informationen zu Bewertungsmethoden finden Sie unter Feature Selection (Data Mining).
ARIMA: Die Bayesian Information Criterion (BIC)-Bewertung des ARIMA-Modells. Die gleiche Bewertung wird für alle ARIMA-Knoten im Zusammenhang mit der Formel festgelegt.
MSOLAP_KNOTEN_KURZBESCHREIBUNG
ARTXP: Dieselben Informationen wie die NODE_DESCRIPTION.
ARIMA: Dieselben Informationen wie die NODE_CAPTION: d. h. die kurze Form der ARIMA-Formel.
Verständnis des ARTXP-Baums
Das ARTXP-Modell trennt deutlich die Bereiche der Daten, die linear von den Bereichen der Daten sind, die sich auf einen anderen Faktor aufteilen. Unabhängig davon, wo die Änderungen im vorhersagbaren Attribut direkt als Funktion der unabhängigen Variablen dargestellt werden können, wird eine Regressionsformel berechnet, um diese Beziehung darzustellen.
Wenn beispielsweise für die meisten Datenreihen eine direkte Korrelation zwischen Zeit und Umsatz besteht, würde jede Datenreihe innerhalb einer Zeitreihenstruktur (NODE_TYPE =16) enthalten sein, die für jede Datenreihe keine untergeordneten Knoten enthält, nur eine Regressionsgleichung. Wenn die Beziehung jedoch nicht linear ist, kann ein ARTXP-Zeitreihebaum Bedingungen in untergeordnete Knoten aufteilen, genau wie ein Entscheidungsbaum-Modell. Indem Sie den Modellinhalt in der Microsoft Generic Content Tree Viewer anzeigen, können Sie sehen, wo die Unterbrechungen auftreten und wie sich dies auf die Trendlinie auswirkt.
Um dieses Verhalten besser zu verstehen, können Sie das im Basic Data Mining Tutorial erstellte Zeitreihenmodell überprüfen. Dieses Modell, das auf dem AdventureWorks Data Warehouse basiert, verwendet keine besonders komplexen Daten. Daher gibt es in der ARTXP-Struktur nicht viele Teilungen. Selbst dieses relativ einfache Modell veranschaulicht jedoch drei verschiedene Arten von Splits:
Die Trendlinie [Amount] für die Region "Pazifik" teilt sich auf den Zeitschlüssel. Eine zeitliche Unterbrechung bedeutet, dass sich der Trend zu einem bestimmten Zeitpunkt ändert. Die Trendlinie war nur bis zu einem bestimmten Punkt linear, und dann nahm die Kurve eine andere Form an. Beispielsweise kann eine Zeitreihe bis zum 6. August 2002 fortgesetzt werden, und eine andere Zeitreihe beginnt nach diesem Datum.
Die Trendlinie [Amount] für die Region Nordamerika wird basierend auf einer weiteren Variablen aufgeteilt. In diesem Fall teilt sich der Trend für Nordamerika auf der Grundlage des Werts desselben Modells im europäischen Raum. Mit anderen Worten, der Algorithmus hat festgestellt, dass sich der Wert für Nordamerika A auch ändert, wenn sich der Wert für Europa ändert.
Die Trendlinie für die Region Europa kreuzt sich selbst.
Was bedeutet jede Aufteilung? Die Interpretation der informationen, die vom Modellinhalt vermittelt werden, ist eine Kunst, die ein tiefes Verständnis der Daten und ihrer Bedeutung im Geschäftskontext erfordert.
Die offensichtliche Verbindung zwischen den Trends für die Regionen Nordamerika und Europa kann nur bedeuten, dass die Datenreihe für Europa mehr Entropie aufweist, was dazu führt, dass der Trend für Nordamerika schwächer erscheint. Oder es kann keinen signifikanten Unterschied in der Bewertung für die beiden geben, und die Korrelation könnte versehentlich sein, basierend auf der Berechnung Europas vor dem Berechnen von Nordamerika. Möglicherweise möchten Sie die Daten jedoch überprüfen und sicherstellen, ob die Korrelation falsch ist, oder prüfen Sie, ob ein anderer Faktor beteiligt sein könnte.
Die Aufteilung des Zeitschlüssels bedeutet, dass es eine statistisch signifikante Änderung des Steigungswinkels der Linie gibt. Dies könnte durch mathematische Faktoren wie die Unterstützung für jeden Bereich oder die Berechnungen von Entropie verursacht werden, die für die Aufteilung erforderlich sind. Daher könnte diese Aufteilung in Bezug auf die Bedeutung des Modells in der realen Welt nicht interessant sein. Wenn Sie jedoch den in der Aufteilung angegebenen Zeitraum überprüfen, finden Sie möglicherweise interessante Korrelationen, die nicht in den Daten dargestellt werden, z. B. eine Verkaufsaktion oder ein anderes Ereignis, das zu diesem Zeitpunkt begonnen hat und die die Daten möglicherweise beeinflusst haben.
Wenn die Daten zusätzliche Attribute enthielten, würden Sie sehr wahrscheinlich interessantere Beispiele für die Verzweigung in der Baumstruktur sehen. Wenn Sie beispielsweise Wetterinformationen nachverfolgt und diese als Attribut für die Analyse verwendet haben, werden möglicherweise mehrere Aufspaltungen im Baum angezeigt, die die komplexe Wechselwirkung zwischen Verkaufszahlen und Wetter darstellen.
Kurz gesagt, Data Mining ist nützlich, um Hinweise darauf zu geben, wo potenziell interessante Phänomene auftreten, aber weitere Untersuchungen und die Expertise der Geschäftsbenutzer sind erforderlich, um den Wert der Informationen im Kontext genau zu interpretieren.
Elemente der ARTXP-Zeitreihenformel
Zum Anzeigen der vollständigen Formel für eine ARTXP-Struktur oder -Verzweigung empfiehlt es sich, die Mininglegende des Microsoft Time Series Viewers zu verwenden, die alle Konstanten in einem lesbaren Format darstellt.
Der folgende Abschnitt enthält eine Beispielgleichung und erläutert die grundlegenden Begriffe.
Mininglegende für eine ARTXP-Formel
Das folgende Beispiel zeigt die ARTXP-Formel für einen Teil des Modells, wie in der Mininglegende dargestellt. Um diese Formel anzuzeigen, öffnen Sie das [Prognose]-Modell, das Sie im Lernprogramm "Grundlegendes Data Mining" im Microsoft Time Series Viewer erstellt haben, klicken Sie auf die Registerkarte " Modell ", und wählen Sie die Struktur für die Datenreihe R250: Europe aus.
Um die formel anzuzeigen, die für dieses Beispiel verwendet wird, klicken Sie auf den Knoten, der die Datumsreihe am oder nach dem 5.07.2003 darstellt.
Beispiel für eine Gleichung eines Baumknotens:
Menge = 21,322
-0,293 * Menge(R250 Nordamerika,-7) + 0,069 * Menge(R250 Europa,-1) + 0,023 *
Menge(R250 Europa,-3) -0,142 * Menge(R750 Europa,-8)
In diesem Fall stellt der Wert 21,322 den Wert dar, der für "Quantity" als Funktion der folgenden Elemente der Formel vorhergesagt wird.
Ein Element ist z. B. "Quantity(R250 North America,-7"). Diese Schreibweise bedeutet die Menge für die Region Nordamerika bei t-7 oder sieben Zeitsegmenten vor dem aktuellen Zeitsegment. Der Wert für diese Datenreihe wird mit dem Koeffizienten -0,293 multipliziert. Der Koeffizienten für jedes Element wird während des Schulungsvorgangs abgeleitet und basiert auf Trends in den Daten.
Es gibt mehrere Elemente in dieser Gleichung, da das Modell berechnet hat, dass die Menge des Modells R250 in der Region Europa von den Werten mehrerer anderer Datenreihen abhängt.
Modellinhalt für eine ARTXP-Formel
Die folgende Tabelle enthält die gleichen Informationen für die Formel, wobei der Inhalt des relevanten Knotens verwendet wird, wie im Microsoft Generic Content Tree Viewer (Data Mining) angezeigt.
| ATTRIBUTE_NAME | ATTRIBUT_WERT | Alias | WAHRSCHEINLICHKEIT | ABWEICHUNG | WERTTYP |
|---|---|---|---|---|---|
| Menge(R250 Europe, y-Achsenabschnitt) | 21.3223433563772 | 11 | 0 | 1.65508795539661 | 11 (Abschnitt) |
| Menge(R250 Europa,-1) | 0.0691694140876526 | 0 | 0 | 0 | 7 (Koeffizient) |
| Menge(R250 Europa,-1) | 20.6363635858123 | 0 | 0 | 182.380682874818 | 9 (Statistik) |
| Menge(R750 Europa,-8) | -0.1421203048299 | 0 | 0 | 0 | 7 (Koeffizient) |
| Menge(R750 Europa,-8) | 22.5454545333019 | 0 | 0 | 104.362130048408 | 9 (Statistik) |
| Menge(R250 Europa,-3) | 0.0234095979448281 | 0 | 0 | 0 | 7 (Koeffizient) |
| Menge(R250 Europa,-3) | 24.8181818883176 | 0 | 0 | 176,475304989169 | 9 (Statistik) |
| Menge(R250 Nordamerika,-7) | -0.292914186039869 | 0 | 0 | 0 | 7 (Koeffizient) |
| Menge(R250 Nordamerika,-7) | 10.36363640433 | 0 | 0 | 701.882534898676 | 9 (Statistik) |
Wie Sie aus dem Vergleich dieser Beispiele sehen können, enthält der Miningmodellinhalt dieselben Informationen, die in der Mininglegende verfügbar sind, aber mit zusätzlichen Spalten für Varianz und Unterstützung. Der Wert für die Unterstützung gibt die Anzahl der Fälle an, die den in dieser Formel beschriebenen Trend unterstützen.
Verwenden der ARTXP-Zeitreihenformel
Für die meisten Geschäftsbenutzer besteht der Wert des ARTXP-Modellinhalts darin, dass er sowohl eine Strukturansicht als auch eine lineare Darstellung der Daten kombiniert.
Wenn die Änderungen im vorhersagbaren Attribut als lineare Funktion der unabhängigen Variablen dargestellt werden können, berechnet der Algorithmus automatisch die Regressionsgleichung und gibt diese Datenreihe in einem separaten Knoten aus.
Wenn die Beziehung nicht als lineare Korrelation ausgedrückt werden kann, verzweigt die Zeitreihe wie eine Entscheidungsstruktur.
Indem Sie den Modellinhalt im Microsoft Time Series Viewer durchsuchen, können Sie sehen, wo die Unterbrechung auftritt und wie sich dies auf die Trendlinie auswirkt.
Wenn eine direkte Korrelation zwischen Zeit und Umsatz für einen Teil der Datenreihe besteht, besteht die einfachste Möglichkeit zum Abrufen der Formel darin, die Formel aus der Mininglegende zu kopieren und dann in ein Dokument oder eine Präsentation einzufügen, um das Modell zu erläutern. Alternativ können Sie den Mittelwert, den Koeffizienten und andere Informationen aus der NODE_DISTRIBUTION-Tabelle für diesen Baum extrahieren und verwenden, um Fortsetzungen des Trends zu berechnen. Wenn die gesamte Datenreihe eine konsistente lineare Beziehung aufweist, ist die Formel im Knoten (Alle) enthalten. Wenn es irgendeine Verzweigung im Baum gibt, ist die Gleichung im Blattknoten enthalten.
Die folgende Abfrage gibt alle ARTXP-Blattknoten aus einem Miningmodell zusammen mit der geschachtelten Tabelle NODE_DISTRIBUTION zurück, die die Formel enthält.
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_NAME,
NODE_CAPTION,
(SELECT ATTRIBUTE_NAME, ATTRIBUTE_VALUE, [VARIANCE], VALUETYPE
FROM NODE_DISTRIBUTION) as t
FROM Forecasting.CONTENT
WHERE NODE_TYPE = 15
Grundlegendes zum ARIMA-Baum
Jede Struktur in einem ARIMA-Modell entspricht einer Periodizität oder periodischen Struktur. Eine periodische Struktur ist ein Muster von Daten, das sich in der gesamten Datenreihe wiederholt. Einige geringfügige Abweichungen im Muster sind innerhalb statistischer Grenzen zulässig. Periodizität wird entsprechend den Standardzeiteinheiten gemessen, die in den Schulungsdaten verwendet wurden. Wenn die Schulungsdaten beispielsweise Verkaufsdaten für jeden Tag bereitstellen, ist die Standardzeiteinheit ein Tag, und alle regelmäßigen Strukturen werden als angegebene Anzahl von Tagen definiert.
Jeder Zeitraum, der vom Algorithmus erkannt wird, erhält seinen eigenen Strukturknoten. Wenn Sie beispielsweise tägliche Verkaufsdaten analysieren, erkennt das Modell möglicherweise periodische Strukturen, die Wochen darstellen. In diesem Fall erstellt der Algorithmus zwei periodische Strukturen im fertigen Modell: eine für den standard täglichen Zeitraum, angegeben als {1}, und eine für Wochen, angegeben durch {7}.
Die folgende Abfrage gibt beispielsweise alle ARIMA-Strukturen aus einem Miningmodell zurück.
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_NAME, NODE_CAPTION
FROM Forecasting.CONTENT
WHERE NODE_TYPE = 27
Beispielergebnisse:
| MODEL_NAME | Attributname | NODE_NAME | NODE_TYPE | NODE_BESCHRIFTUNG |
|---|---|---|---|---|
| Prognose | M200 Europe:Menge | TA00000000 | 27 | ARIMA (1,0,1) |
| Prognose | M200 Nordamerika:Menge | TA00000001 | 27 | ARIMA (1,0,4) X (1,1,4)(6) |
| Prognose | M200 Pacific:Menge | TA00000002 | 27 | ARIMA (2,0,8) X (1,0,0)(4) |
| Prognose | M200 Pacific:Menge | TA00000002 | 27 | ARIMA (2,0,8) X (1,0,0)(4) |
| Prognose | R250 Europe:Menge | TA00000003 | 27 | ARIMA (1,0,7) |
| Prognose | R250 Nordamerika:Menge | TA00000004 | 27 | ARIMA (1,0,2) |
| Prognose | R250 Pacific:Menge | TA00000005 | 27 | ARIMA (2,0,2) X (1,1,2)(12) |
| Prognose | R750 Europa:Menge | TA00000006 | 27 | ARIMA (2,1,1) X (1,1,5)(6) |
| Prognose | T1000 Europe:Menge | TA00000009 | 27 | ARIMA (1,0,1) |
| Prognose | T1000 Nordamerika:Menge | TA00000000a | 27 | ARIMA (1,1,1) |
| Prognose | T1 000 Pacific:Quantity | TA0000000b | 27 | ARIMA (1,0,3) |
Anhand dieser Ergebnisse, die Sie auch mithilfe des Microsoft Generic Content Tree Viewers (Data Mining) durchsuchen können, können Sie auf einen Blick erkennen, welche Serie vollständig linear ist, welche mehrere periodische Strukturen aufweisen und was die ermittelten Periodizitäten sind.
Die kurze Form der ARIMA-Formel für die Serie M200 Europe teilt Ihnen beispielsweise mit, dass nur der standard- oder tägliche Zyklus erkannt wurde. Die kurze Form der Formel wird in der Spalte NODE_CAPTION angegeben.
Für die Serie M200 Nordamerika wurde jedoch eine zusätzliche regelmäßige Struktur gefunden. Der Knoten TA00000001 verfügt über zwei untergeordnete Knoten, einer mit der Formel (1,0,4) und einer mit der Formel (1,1,4)(6). Diese Formeln werden verkettet und im übergeordneten Knoten dargestellt.
Für jede periodische Struktur stellt der Modellinhalt auch die Reihenfolge und den gleitenden Durchschnitt als untergeordnete Knoten bereit. Mit der folgenden Abfrage werden beispielsweise die Kindknoten eines der im vorherigen Beispiel aufgeführten Knoten abgerufen. Beachten Sie, dass die Spalte, PARENT_UNIQUE_NAME, in eckige Klammern eingeschlossen werden muss, um sie vom reservierten Schlüsselwort desselben Namens zu unterscheiden.
SELECT *
FROM Forecasting.CONTENT
WHERE [PARENT_UNIQUE_NAME] = ' TA00000001'
Da es sich um einen ARIMA-Baum handelt, nicht um einen ARTXP-Baum, können Sie die IsDescendant (DMX)-Funktion nicht verwenden, um die untergeordneten Knoten dieser periodischen Struktur zurückzugeben. Stattdessen können Sie die Attribut- und Knotentypen verwenden, um die Ergebnisse zu filtern und die untergeordneten Knoten zurückzugeben, die weitere Details zur Erstellung der Formel bereitstellen, einschließlich der gleitenden Mittelwerte und der Differenzreihenfolge.
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_UNIQUE_NAME,
NODE_TYPE, NODE_CAPTION
FROM Forecasting.CONTENT
WHERE [MSOLAP_MODEL_COLUMN] ='M200 North America:Quantity'
AND (NODE_TYPE = 29 or NODE_TYPE = 30)
Beispielergebnisse:
| MODEL_NAME | ATTRIBUTE_NAME | KNOTEN_EINZIGARTIGER_NAME | NODE_TYPE | NODE_BESCHRIFTUNG |
|---|---|---|---|---|
| Prognose | M200 Nordamerika:Menge | TA00000001000000010 | 29 | ARIMA {1,0.961832044807041} |
| Prognose | M200 Nordamerika:Menge | TA00000001000000011 | 30 | ARIMA {1,-3.51073103693271E-02,2.15731642954099,-0.22031433327742,-1.33151478258758} |
| Prognose | M200 Nordamerika:Menge | TA00000001000000000 | 29 | ARIMA {1,0.643565911081657} |
| Prognose | M200 Nordamerika:Menge | TA00000001000000001 | 30 | ARIMA {1,1.45035399809581E-02,-4.4048928392752E-02,-0.19203901352577,0.242202497643993} |
Diese Beispiele veranschaulichen, dass je weiter man in den ARIMA-Baum geht, desto mehr Details werden offenbar; die wichtigen Informationen werden jedoch auch im übergeordneten Knoten kombiniert und dargestellt.
Zeitreihenformel für ARIMA
Um die vollständige Formel für jeden ARIMA-Knoten anzuzeigen, empfehlen wir, die Mininglegende des Microsoft Time Series Viewers zu verwenden, die die autoregressive Reihenfolge, gleitende Mittelwerte und andere Elemente der Formel darstellt, die bereits in einem konsistenten Format erstellt wurden.
In diesem Abschnitt wird eine Beispielgleichung dargestellt und die grundlegenden Begriffe erläutert.
Mininglegende für ARIMA-Formel
Das folgende Beispiel zeigt die ARIMA-Formel für einen Teil des Modells, wie in der Mininglegende dargestellt. Um diese Formel anzuzeigen, öffnen Sie das Prognosemodell mithilfe der Microsoft Time Series Viewer, klicken Sie auf die Registerkarte " Modell ", wählen Sie die Struktur für die Datenreihe "R250: Europe" aus, und klicken Sie dann auf den Knoten, der die Datumsreihe am oder nach dem 07.5.2003 darstellt. Die Mininglegende verfasst alle Konstanten in einem lesbaren Format, wie im folgenden Beispiel gezeigt:
FORMEL ARIMA:
ARIMA ({1,1},0,{1,1,49791920964142,1,10640053499397,0,888873034670339,-5,05429403071953E-02,-0,905265316720334,-0,961908900643379,-0,649991020901922}) Intercept: 56,8888888888889
Diese Gleichung ist das lange ARIMA-Format, das die Werte der Koeffizienten und des Schnittpunkts enthält. Das kurze Format für diese Gleichung wäre {1,0,7}, wobei 1 die Periode als Anzahl von Zeitabschnitten angibt, 0 gibt die Differenzordnungsbegriff an, und 7 gibt die Anzahl der Koeffizienten an.
Hinweis
Eine Konstante wird von Analysis Services für die Berechnung der Varianz berechnet, die Konstante selbst wird jedoch nicht an einer beliebigen Stelle auf der Benutzeroberfläche angezeigt. Sie können die Varianz für einen beliebigen Punkt in der Datenreihe jedoch als Funktion dieser Konstante anzeigen, wenn Sie in der Diagrammansicht "Abweichungen anzeigen" auswählen. Die Tooltip für jede Datenreihe zeigt die Varianz für einen bestimmten vorhergesagten Punkt an.
Modellinhalt für die ARIMA-Formel
Ein ARIMA-Modell folgt einer Standardstruktur mit unterschiedlichen Informationen, die in Knoten unterschiedlicher Typen enthalten sind. Um den Modellinhalt für das ARIMA-Modell anzuzeigen, ändern Sie den Viewer in den Microsoft Generic Content Tree Viewer, und erweitern Sie dann den Knoten mit dem Attributnamen R250 Europe: Quantity.
Ein ARIMA-Modell für eine Datenreihe enthält die grundlegende periodische Formel in vier verschiedenen Formaten, aus denen Sie je nach Anwendung wählen können.
NODE_CAPTION: Zeigt das kurze Format der Formel an. Das kurze Format gibt an, wie viele periodische Strukturen dargestellt werden und wie viele Koeffizienten sie aufweisen. Wenn beispielsweise das kurze Format der Formel lautet {4,0,6}, stellt der Knoten eine periodische Struktur mit 6 Koeffizienten dar. Wenn das kurze Format etwa {2,0,8} x {1,0,0}(4) ist, enthält der Knoten zwei periodische Strukturen.
KNOTENBESCHREIBUNG: Zeigt das lange Format der Formel an, das auch die Form der Formel ist, die in der Mininglegende angezeigt wird. Die lange Form der Formel ähnelt dem kurzen Formular, mit der Ausnahme, dass die tatsächlichen Werte der Koeffizienten angezeigt werden, anstatt gezählt zu werden.
NODE_RULE: Zeigt eine XML-Darstellung der Formel an. Je nach Knotentyp kann die XML-Darstellung einzelne oder mehrere periodische Strukturen enthalten. In der folgenden Tabelle wird veranschaulicht, wie XML-Knoten auf höheren Ebenen des ARIMA-Modells zusammengefasst werden.
| Knotentyp | XML-Inhalt |
|---|---|
| 27 (ARIMA-Stamm) | Enthält alle periodischen Strukturen für die Datenreihe und den Inhalt aller untergeordneten Knoten für jede periodische Struktur. |
| 28 (ARIMA Periodische Struktur) | Definiert eine einzelne periodische Struktur, einschließlich des autoregressiven Termknotens und der gleitenden Mittelwertkoeffizienten. |
| 29 (ARIMA Autoregressive) | Listet die Begriffe für eine einzelne periodische Struktur auf. |
| 30 (ARIMA Gleitender Durchschnitt) | Listet die Koeffizienten für eine einzelne periodische Struktur auf. |
NODE_DISTRIBUTION: Zeigt Ausdrücke der Formel in einer geschachtelten Tabelle an, die Sie abfragen können, um bestimmte Ausdrücke abzurufen. Die Knotenverteilungstabelle folgt der gleichen hierarchischen Struktur wie die XML-Regeln. Das heißt, der Stammknoten der ARIMA-Reihe (NODE_TYPE = 27) enthält den Abfangenwert und die Periodizitäten für die vollständige Formel, die mehrere Periodizitäten enthalten kann, während die untergeordneten Knoten nur Informationen enthalten, die für eine bestimmte periodische Struktur oder für die untergeordneten Knoten dieser periodischen Struktur spezifisch sind.
| Knotentyp | Merkmal | Werttyp |
|---|---|---|
| 27 (ARIMA-Stamm) | AchsenAbschnitt Periodizität |
11 |
| 28 (ARIMA Periodische Struktur) | Periodizität Automatische regressive Reihenfolge Reihenfolge der Unterschiede Ordnung des gleitenden Durchschnitts |
12 13 15 14 |
| 29 (ARIMA Autoregressive) | Koeffizient (Komplement des Koeffizienten) |
7 |
| 30 (ARIMA Gleitender Durchschnitt) | Wert zum Zeitpunkt t Wert bei t-1 ... Wert bei t-n |
7 |
Der Wert für die Reihenfolge des gleitenden Mittelwerts gibt die Anzahl der gleitenden Mittelwerte in einer Datenreihe an. Im Allgemeinen wird der gleitende Mittelwert n-1 mal berechnet, wenn es n Begriffe in einer Datenreihe gibt, aber die Zahl kann für eine einfachere Berechnung reduziert werden.
Der Wert für die autoregressive Reihenfolge gibt die Anzahl der autoregressiven Datenreihen an.
Der Wert für die Differenzreihenfolge gibt an, wie oft die Datenreihe verglichen oder differenziert ist.
Eine Aufzählung der möglichen Werttypen finden Sie unter "Microsoft.AnalysisServices.AdomdServer.MiningValueType".
Verwenden der ARIMA-Bauminformationen
Wenn Sie Vorhersagen verwenden, die auf dem ARIMA-Algorithmus in einer Geschäftslösung basieren, sollten Sie die Formel in einen Bericht einfügen, um die Methode zu veranschaulichen, die zum Erstellen der Vorhersage verwendet wurde. Mit der Beschriftung können Sie die Formeln im kurzen Format präsentieren, oder die Beschreibung, um die Formeln im langen Format darzustellen.
Wenn Sie eine Anwendung entwickeln, die Zeitreihenvorhersagen verwendet, ist es möglicherweise hilfreich, die ARIMA-Formel aus dem Modellinhalt abzurufen und dann Eigene Vorhersagen zu erstellen. Um die ARIMA-Formel für eine bestimmte Ausgabe abzurufen, können Sie den ARIMA-Stamm für dieses bestimmte Attribut direkt abfragen, wie in den vorherigen Beispielen gezeigt.
Wenn Sie die ID des Knotens kennen, der die gewünschte Datenreihe enthält, haben Sie zwei Optionen, um die Komponenten der Formel abzurufen:
Geschachteltes Tabellenformat: Verwenden Sie eine DMX-Abfrage oder eine Abfrage über den OLEDB-Client.
XML-Darstellung: Verwenden Sie eine XML-Abfrage.
Bemerkungen
Es kann schwierig sein, Informationen aus einem ARTXP-Baum abzurufen, da sich die Informationen zu jeder Teilung an einem anderen Ort innerhalb des Baums befinden. Daher müssen Sie mit einem ARTXP-Modell alle Teile abrufen und dann eine Verarbeitung durchführen, um die vollständige Formel zu rekonstituieren. Das Herleiten einer Gleichung aus einem ARIMA-Modell ist einfacher, da die Formel durchgängig in der Baumstruktur verfügbar gemacht wurde. Informationen zum Erstellen einer Abfrage zum Abrufen dieser Informationen finden Sie unter Beispiele für Zeitreihenmodellabfragen.
Siehe auch
Inhalt des Mining-Modells (Analysis Services - Data Mining)
Microsoft-Zeitreihenalgorithmus
Abfragebeispiele für Zeitreihenmodelle
Technische Referenz zu Microsoft-Zeitreihenalgorithmus